본 포스팅의 주제는 데이타비트의 갯수가 정해질 때, 몇 개 의 패러티 비트를 전달해야 코드워드의 1 비트 오류에 대해서 자동정정이 가능한가에 대한 이야기이다.
먼저 아래의 코드워드를 가진 해밍코드가 있다고 하자.
$$n=t+r \text{ —– 식 (1)} $$
여기서, $n$: 코드워드의 비트 갯수, $t$:원데이타 코드의 비트 갯수, $r$:패러티비트의 갯수다.
그리고, 해밍거리에 대해서 알아야 한다. 해밍거리는 문자열과 문자열의 비교 후, 동일한 값을 가지도록 하는 경우의 최소 수이다.
Hello와 Hellu의 해밍거리는? 1이다. 문자 1개만 바꾸면 되기 때문에 해밍거리는 1이다.
etllo tello의 해밍거리는? 문자 2개를 바꾸기 때문에 해밍거리는 2다.
000과 111의 해밍거리는? 문자 3개를 바꾸기 때문에 해밍거리는 3이다.
2진수 3비트에서 몇 개 더 해보자.
010과 111 => 해밍거리 2
011과 101 => 해밍거리 2
그러면 3비트의 최대거리는 (0,0,0)과 (1,1,1)에서 해밍거리는 3비트가 만들어 내는 최대의 거리 3 해밍거리를 가진다. 두 개의 문자열을 동일하게 바꾸기 위한 방법이 각 비트를 하나씩 변경하면서 만들면 된다.
아래 그림을 보면 이해할 수 있을 것이다.
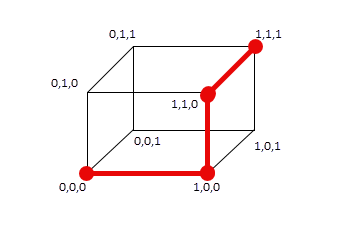
즉, 해밍거리라고 하면 2 지점간의 최소거리를 항상 의미한다.
그러므로 아래처럼 가는 것은 해밍거리 5라고 하지 않는다.
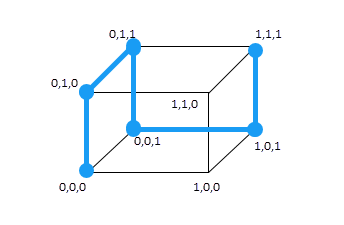
해밍거리와 최소해밍거리를 자주 혼동해서 말하는데, 해밍거리는 단지 2 개의 코드 사이의 거리이다.
최소해밍거리는 해밍이 이루어 질 수 있는 거리, 즉 오류발생유무 확인 또는 오류자동정정이 가능한 거리를 말한다. 즉, 최소해밍거리는 유효코드와 유효코드와의 거리 중, 최소 거리를 뜻해서 최소해밍거리라고 불린다.
| 구분 | 해밍거리($d$) | 최소 해밍거리($d_min$) |
| 대상 | 두 개의 특정 코드 | 여러 개의 코드 집합 중에서 |
| 의미 | 두 코드 사이의 각 비트의 차잇 값 | 유효 코드와 다른 유효 코드와의 거리 |
| 목적 | 단순 거리 측정 | 에러 정정 능력이 있음을 확인 |
| 예 | 해밍거리=1. (0,0,0) -> (1,0,0) | 최소 해밍거리=3. (0,0,0) -> (1,1,1) |
표 1. 해밍거리와 최소 해밍거리의 차이
예를 들면,
그림 1에서 정육각형의 각 모서리는 8개의 꼭지점을 가지고 있다. 각 꼭지점은 고유한 값으로 표현된다. 그러므로, 이 집합에서 각 꼭지점과 다른 꼭지점과의 해밍거리는 1이된다. 단, 최소해밍거리는 $d_{min}=3$이다. 이는 유효 코드(0,0,0)와 다른 유효코드(1,1,1)과의 해밍거리다.
즉, 최소해밍거리는 기준이 되는 지점(코드)과 하나의 비트가 차이가 나는 지점(코드)와의 거리이다. 그림 1을 보면 시작점에서 끝 점까지 항상 해밍거리를 유지하면서 이동함을 볼 수 있다.
위에서 일반적인 해밍코드(최소해밍코드, 거리)에 대한 개념을 이해했다면, 이제는 데이타 비트가 1일 때 패러티비트 갯수 2개로 에러정정이 정말로 가능한지 알아봐야 겠다.
먼저 아래의 표를 만들 수 있다.
(저 번 포스팅에서 1개의 데이터 비트와 한 개의 패러티비트로는 오류발생유무는 알아도, 오류발생위치는 알 수 없음에 대해서 공부했다.)
| $d_1$ | $p_1$ | $p_2$ | 유효 코드워드 |
| 0 | 0 | 0 | 000 |
| 1 | 1 | 1 | 111 |
표 2. 3비트 코드워드의 유효 코드워드
윗 표와 같이 유효코드와의 해밍거리는 3이된다. 즉, 윗 코드워드의 최소해밍거리는 3이된다.
아래의 더보기를 누르면 4비트 코드워드에서 최소해밍거리를 찾는 표를 보인다.
이번엔 4비트로 해보자. 코드워드는 각각 2개의 데이타 비트와 패러티 비트이다.
| $d_1$ | $d_2$ | $p_1 = EV(d_1, d_2)$ | $p_2 = EV(d_1, d_2)$ | 유효 코드워드 |
| 0 | 0 | 0 | 0 | 0000 |
| 0 | 1 | 1 | 1 | 0111 |
| 1 | 0 | 1 | 1 | 1011 |
| 1 | 1 | 0 | 0 | 1100 |
표. 4비트(데이타 2 비트, 패러티 2 비트) 시스템
0000, 0111 > 해밍거리3
0111,1011 > 해밍거리2
1011, 1100 > 해밍거리 3
1100, 0000 > 해밍거리2
그러므로 해밍거리2가 최소해밍거리가 된다.
그러므로 위 시스템은 오류정정은 해밍거리1에서 가능하나 오류발생확인은 해밍거리2에서는 불가능함을 알 수 있다.
(1비트에서 오류 정정 가능, 2비트에서 오류 발생 확인 불가능)
계속 설명하자면, 아래와 같이 하나의 비트만 에러가 난 해밍거리1인 코드표를 만든다. 이러면 이 해밍거리 1인 코드는 가장 가까운 유효코드워드로 변경(정정)이 가능함을 알 수 있다. 즉, 각각의 유효 코드워드에서 해밍거리 1인 코드를 찾아서 표로 만들라는 이야기다.
| $d_1$ | $p_1$ | $p_2$ | 유효 코드워드 | 유효 코드워드와의 해밍거리1인 코드 |
| 0 | 0 | 0 | 000 | 001, 010, 100 |
| 1 | 1 | 1 | 111 | 110, 101, 011 |
표 3. 3비트 코드워드의 유효 코드워드와 1비트 차이나는 해밍거리 1인 코드
이것을 오류정정능력이라 하자.
그리고, 오류 발생 유무는 (0,0,0)에서는 (110), (101), (011)이 되고, (1,1,1)에서는 (001), (010), (100)이 된다. 즉, 거리 2다. 이것은 유효 코드워드 (0, 0, 0)에서 2개 비트가 바뀐것도 유효 코드워드 (1,1,1)에서 1비트만 바뀐것과 같으므로 오류로 판정할 수 있다는 것이다.
(단, 2 개의 오류가 발생해도 해밍거리=1인 것이라고 판단, 1 개의 오류만 정정한 것은 올바른 답이라고는 할 수 없으나, 오류라고는 판정할 수 있기 때문에 이것은 오류감지능력이라 할 수 있다.
윗 내용을 정리하면,
오류정정능력: 최소해밍거리와 관련이 있다. 최소해밍거리=3에서는 해밍거리1의 코드워드를 정정할 수 있다. 만일 최소해밍거리=4라면, 2해밍거리의 코드워드를 정정할 수 있을 것이다. 왜냐면, 가장 가까운 유효코드로
오류감지능력: 유효코드워드 (0,0,0)과 (1,1,1)의 최소해밍거리($d$)는 3이다. 그래서 $2$ 개의 비트에서 오류가 발생하면, 오류를 감지할 수 있게 된다. 만일 3개의 비트에서 에러가 발생되면 이것은 다른 유효코드워드 값이 되기 때문에 에러를 감지할 수 없다. 그러므로 오류감지능력은 최소해밍거리에서 한 개를 빼준값이 된다. $3-1=2$.
그런데 이것을 표 2.와 표 3.으로 로 보면 한 눈에 들어오는데, 그런데 이것을 일반화해서 사용할 수 있을까라는 의문이 든다.
먼저 그림 3. 을 보자. 이 그림을 보면, 1개 오류가 발생토록 해밍거리는 d=1이다. 그것은 A유효코드워드와 B유효코드의 굵은 선으로 둘러쌓인 반지름이 k=1인 각각의 원이된다. 이 때의 반지름을 일반화해서 패킹반경(k)라고 정의해보자. 단, 패킹반경은 정수이다.
그런데 패킹반경이 2면 어떨까? 패킹반경이 2라는 이야기는 해밍거리가 1과 2인 코드들을 각 A, B가 포함한다는 의미이다. 그래서 그림 3.을 보듯이 해밍거리 1인 코드들과 해밍거리 2인 코드들이 교집합상태가 된다. 그러므로 패킹거리 k=2까지는 오류감지능력이 발생한다고 말 할 수 있다.
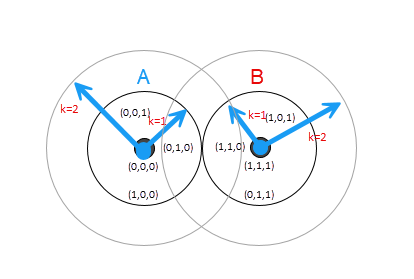
그런데 패킹거리가 3이되면 어떻케 될까? 패킹거리가 3이면, 이는 다른 유효코드를 포함하게 된다. 최소해밍거리(d)가 3이면, 3개의 비트가 변경될 때 다른 유효코드워드로 바뀌게 되어, 오류감지를 할 수 없게 된다고 이야기 한 것을 기억하는가?
그러므로 아래의 수식이 성립하게 된다.
$$k+k < d$$
여기서 부등호를 넣은 이유는 $2k$ 값이 $d$와 같다면, 코드워드가 동일해지기 때문이다.
그런데 $\leq$로 표시하고 싶다. 이러면 1을 더해주면 된다. (여러 지식사이트에서 아랫 수식을 유도하면서 열심히 설명해 주던데 그냥 이렇케 이해 했다.)
$$2k+1 \leq d \text{ —– 식 (2)}$$
식 (2)를 $k$에 대해서 정리하면,
$$k \leq \frac{ d-1}{2} \text{ —– 식 (3)}$$
수식 (3)은 최소해밍거리를 알 때의 오류정정능력을 보여준다. 즉, 최소해밍거리를 알면 패킹거리(오류 정정 가능 거리)를 구하는 공식이 된다.
식을 $d$에 대해서 정리하면,
$$d \geq 2k +1 \text{ —– 식 (4)}$$
식 (4)는 패킹거리를 알면 최소해밍거리를 구하는 공식이다. 즉, 오류 정정이 가능한 비트를 설정해주면, 최소해밍거리인 유효코드워드의 비트수를 구하는 공식이 된다.
그리고 본 포스팅의 주제라고 서두에서 언급한, 몇 개의 패러티가 필요하다라는 말을 저리 쉽게 하는 이유는 아래 일반식을 유도함을로써 보이겠다.
우리는 $t$ 개의 데이타비트와 $r$ 개의 패러티비트를 사용하여 1비트 오류정정이 가능한 코드워드를 사용하는 시스템을 설계하려고 한다. 그러므로 코드워드의 길이를 $n$이라고 했으므로,
코드워드의 길이: $n=t+r$
그러므로 수식 (4)에 의해서 $k=1$이므로 최소해밍거리($d \geq3$)는 3이상이다.
전제1. 여기서 코드워드가 만들어내는 n비트의 경우의 갯수는 $2^n$ 개가 있다.
전제2. 유효코드워드를 중심에 두고 이 유효코드워드의 1비트가 변화하는 경우의 수는 $n$ 개가 있다. 그러므로, 이것은 각 유효코드워드의 패킹반경 $k=1$을 가지는 원 내부에 있는 코드이며 원 내부의 코드 갯수는 $1+n$ 개이다.
전제3. 유효코드워드의 갯수는 데이타비트가 만들 수 있는 경우의 수와 동일하다. 그러므로 유효코드워드의 갯수는 $2^t$ 개이다.
그러므로 아래의 부등식은 항상 성립해야 한다.
(각 구의 크기) X (유효 코드워드의 갯수) $\leq$ (전체 코드워드의 갯수)
(나 자신 + 한 비트만 변하는 크기) X (유효 코드워드의 갯수) $\leq$ (전체 코드워드의 갯수)
$(1+n) \times (2^{t}) \leq 2^{n} \text{ —– 식 (5)}$
수식 (5)에서 $n=t+r$을 대입하면,
$(1+t+r) \times (2^{t}) \leq 2^{t+r} \text{ —– 식 (6)}$
양변을 $2^t$로 나누면,
$(1+t+r) \leq 2^{r} \text{ —– 식 (7)}$
이 부등식이 바로, 데이타비트의 갯수 t 개를 보호하기 위해 필요한 최소 패러티비트의 갯수를 구하는 식이다.
해보자.
문제. 1개의 데이타 비트를 보호하기 위해 필요한 최소 패러티의 갯수는?
풀이. t=1을 수식 (6)에 대입한다.
$1+1+r \leq 2^r$
$2+r \leq 2^r \text{ —– 식 (8)}$
$r=1, 2+1 \leq 2$ ==> 성립안함.
$r=2, 2+2 \leq 4$ ==> 성립
$r=3, 2+3 \leq 8$ ==> 성립
그러므로 최소 패러티 갯수는 2비트이다.
윗 내용을 숙지하였다면, 아래의 해밍코드를 더 쉽게 이해할 수 있을 것 같다.