데이타 전송 시 1비트의 에러를 정정할 수 있는 오류정정부호의 일종이며 벨 연구소의 Hamming에 의해서 고안되었다. 저장장치의 데이타 입출력에 사용된 기술이다.
위 해밍코드는 패러티체크 기술을 바탕으로 한다. 패러티체크 기술이란 특정 비트수로 표현되는 원데이타의 2진수에서 1의 갯수를 짝수 혹은 홀수로 정해서 고정 코드워드로 통신하는 방법이다. 여기서 코드워드는 “원데이타+패러티비트”로 구성된다. (코드워드 대신에 프레임으로 쓰려다 프레임은 하드웨어의 제어코드까지 포함되므로 일단 코드워드로 불렀다.)
패러티 기술은 조선 시대 인편으로 금 한 돈씩을 매일 대전에서 마포로 보내야 할 일이 있다고 할 때 사용하면 유용했을 것이다. 내가 금을 보내면 그 날짜에 1을 기입, 보내지 않으면 0을 기입한다. 그러면 7일 동안 보낸 1의 갯수가 홀수면 8일 째에 금을 보낸다. 만일 짝수였으면 금을 보내지 않는다.
그래서 매 8 일째, 수신측에서는 금의 짝/홀 수에 따라서 배송이 잘 이루어졌는지를 판별할 수 있는 것이다.
(통신에서는 다시 보내! 하면 된다. 단, 금 한돈이 아니라 두 돈을 빼돌렸다면 도난 당했는지는 알 수 없다는 점은 큰 단점이다.)
이것은 짝수 패러티 체크(Even Pariy Check) 방법과 동일함을 알 수 있다.
예) 짝수 패러티(Even Parity) 체크 방법
원데이타: 1001 1100 + 패러티: 0
송신데이타(코드워드(원데이타 + 패러티)) = 1001 1100 0
송신측에서는 패러티를 자동으로 만들어 내는데 이것은 원 메시지의 MSB 부터 꺼내어 왼쪽 시프트하면서 각 비트와 XOR연산하면 된다. (홀수개의 1이면 1이 되고, 짝수개의 1이 있으면 0이 된다.)
수신측에서는 송신데이타의 1의 갯수를 파악한다. 파악 방법은 송신측에서의 연산과 같은 처리를 해주면 된다.결과가 영(0)이면 오류가 없음을, 영이 아니고 일(1)이면 에러가 발생했음을 알리는 식이다.
이상이 짝수 패러티 체크 방법을 사용한 예이다.
여기서 다시한 번 코드워드를 언급해주자면, 코드워드는 Data 비트와 Parity 비트로 만들어진다. 그리고 코드워드의 갯수(n)=원데이타의 갯수(k)+패러티의 갯수(r)이다.
그런데 이 방법(패러티 체크 방법)은 오류 발생은 알아도 발생된 오류가 어디서 발생했는지와 그 오류를 정정해 줄 수 있는 방법이 없다. 즉, 에러정정 방법이 없다.
(심부름한 사람한테 너 몇일날 금 안가져왔으니 채워놔! 이런 말 하고 싶은거다.)
즉, 수신단에서 통신 중 발생한 오류에 대해서 자동으로 정정해줄 수 있는 코드가 필요했는데 그걸 만든 사람이 바로 해밍이고 그것이 해밍코드다.
단, 해밍코드를 바로 들어가기 전에, 전에 오류정정코드를 어떻케 만들었을까라는 고민을 한 번 해보자.
해밍코드가 단일 비트 오류에 대한 오류 발생 유무 및 오류 발생 비트의 위치 파악이 목적이라고 했다. 그러므로 이 코드는 오류를 나타내는 코드와 위치를 나타내는 코드를 표현할 수 있어야 한다.
먼저 1 비트 데이타를 2 비트 코드워드로 보내는 경우를 생각해보자. 하나의 데이타비트에 하나의 패러티를 넣었다고 가정하자는 말이다.
그러므로 송신단에서의 인코딩은 아래 두 가지 뿐이 없다.
| 데이타($d_1$) | 패러티($p_1$) | 유효 코드워드 |
| 0 | 0 | 00 |
| 1 | 1 | 11 |
표 1. 송신단에서의 유일한 인코딩 값
그러므로 수신단에서도 위 코드워드를 제외한 신호는 잘못되었다는 바로 알 수 있게된다.
즉, 수신단에서 에러 발생을 고려한, 수신 가능한 코드워드의 경우의 수는 4, 위치는 2개, 발생유무는 1개로 쓸 수 있다.
| 데이타($d_1$) | 패러티($p_1$) | 코드워드 | 비고 |
| 0 | 0 | 00 | 정상 |
| 0 | 1 | 01 | ERROR. 1번 또는 2번 비트 오류. |
| 1 | 0 | 10 | ERROR. 1번 또는 2번 비트 오류. |
| 1 | 1 | 11 | 정상 |
표 2. 수신단에서의 코드워드
즉, 위 코드워드로는 발생위치를 알 수 없다.
그럼 1비트 데이타에 2 개의 패러티비트를 추가해서 넣어볼까? 그러면 아래 조건이 만족되어야 한다.
$p_1=p_2$
즉, 송신단에서의 인코딩은 아래 두 가지 뿐이 없다.
| 데이타($d_1$) | 패러티($p_1$) | 패러티($p_2$) | 유효 코드워드 |
| 0 | 0 | 0 | 000 |
| 1 | 1 | 1 | 111 |
표 3. 송신단에서의 유일한 인코딩 값
그리고 에러발생을 염두에두고 수신단에서의 수신 코드를 조사해보면,
| 데이타($d_1$) | 패러티1($p_1$) | 패러티2($p_2$) | 코드워드 | 비고 (하나의 비트 만 에러가 발생하므로 000 또는 111) |
| 0 | 0 | 0 | 000 | 정상 |
| 0 | 0 | 1 | 001 | Error / 000 / 3번 위치 Error |
| 0 | 1 | 0 | 010 | Error / 000 / 2번 위치 Error |
| 0 | 1 | 1 | 011 | Error / 111 / 1번 위치 Error |
| 1 | 0 | 0 | 100 | Error / 000 / 1번 위치 Error |
| 1 | 0 | 1 | 101 | Error / 111 / 2번 위치 Error |
| 1 | 1 | 0 | 110 | Error / 111 / 3번 위치 Error |
| 1 | 1 | 1 | 111 | 정상 |
표 4. 수신단에서의 코드워드
위 표 4.를 보니 1 개의 데이타비트와 2 개의 패러티비트를 조합한 3비트의 코드워드를 사용했더니, 오류정정위치를 판단할 수 있음을 알 수 있다.
아래 링크를 클릭하면, 윗 표를 만들지 않고 데이타비트의 갯수가 정해지면, 1비트 오류를 판정할 수 있게 하는 패러티비트의 갯수를 정할 수 있다.
————————————————————————————–
아래 링크는 표 4.를 만들지 않고 데이타비트의 갯수가 정해지면 최소 패러티갯수를 구할 수 있는 방법을 설명한다.
————————————————————————————–
그런데 매번 저렇케 하나씩 표를 만들어서 오류정정 위치 및 오류임을 판정해야 하는가? 먼가 좋은 방법이 없을까?
바로 그 방법을 설명하고자 한다.
먼저, 신드롬이라는 것을 만들어보자. 신드롬은 증후군이라고 하는데 두 개의 비트를 XOR 연산하면 된다. 이는 같은 종류이면 증후군에 속해있고, 다른 종류이면 증후군에 속해있지 않다고 말하는데서 신드롬이라는 것으로 용어 정의가 된 것 같다. 즉, 앞 비트와 뒷 비트간의 증후를 보고서 에러의 유무와 에러 발생 위치를 찾겠다는 것이다. 즉, 신드롬은 아래와 같다.
$S_1=XOR(d_1, p_1)$
$S_2=XOR(d_1, p_2)$
여기서 $XOR(A, B)$는 $A\text{ xor }B$를 의미한다.
위에서 보면 $d_1$과 $ p_1$은 같아야 한다. 왜냐하면 하나의 비트와 그 패러티 비트는 같아져야 하기 때문이다. 즉, 문제가 발생하면 값이 1이 되면서 신드롬이 깨진다.
이것을 표 4. 에 추가하면 아래의 표가 나온다.
| 데이타 | 패러티($p_1$) | 패러티($p_2$) | 코드워드 | $S_1$ | $S_2$ | 비고 |
| 0 | 0 | 0 | 000 | 0 | 0 | 정상 |
| 0 | 0 | 1 | 001 | 0 | 1 | 3번 위치 에러 |
| 0 | 1 | 0 | 010 | 1 | 0 | 2번 위치 에러 |
| 0 | 1 | 1 | 011 | 1 | 1 | 1번 위치 에러 |
| 1 | 0 | 0 | 100 | 1 | 1 | 1번 위치 에러 |
| 1 | 0 | 1 | 101 | 1 | 0 | 2번 위치 에러 |
| 1 | 1 | 0 | 110 | 0 | 1 | 3번 위치 에러 |
| 1 | 1 | 1 | 111 | 0 | 0 | 정상 |
표 5. 수신단에서의 코드워드와 신드롬
신드롬 $S_1$은 1번 비트와 2번 비트와의 변화가 있을 때 1을 표현한다. 신드롬 $S_2$는 1번과 3번과의 변화가 있으면 나타난다.
1번과 2번, 1번과 3번의 변화 순서로 어떻케 비트에러인지 확인할 수 있지?
아마도 이건 아래의 집합 다이어그램을 보면 이해가 가능할 것이다.
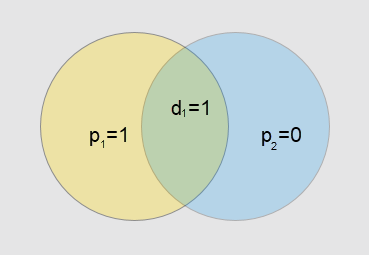
그림 1의 신드롬이 아래와 같으므로
$S_1=XOR(d_1, p_1)$
$S_2=XOR(d_1, p_2)$
신드롬 $S_1$, $S_2$는 신드롬이 깨지는 비트가 1이된다. 그러므로 위치가 2번째 비트가 문제가 있음을 알 수 있다. (각 원에서 1의 갯수는 짝수여야 한다.)
윗 표를 다시 신드롬을 기준으로 변경하면,
| $S_1$ | $S_2$ | $S_1 S_2$ | 에러유무/에러위치 |
| 0 | 0 | 00 | 정상 |
| 0 | 1 | 01 | 에러/3번 |
| 1 | 0 | 10 | 에러/2번 |
| 1 | 1 | 11 | 에러/1번 |
표 6. 수신단에서의 신드롬
오옷! 신드롬 표를 가지고 보니, 신드롬 값에 에러유무와 에러위치를 찾을 수 있다. 그러나, 직관적이지 않다.
바로 그 직관을 해밍이 제시했다.
그의 방법은, 패러티비트를 항상 1과 2의 배수에 두고 그 나머지에 데이타비트를 넣어주면 된다. 해볼까?
($2^r$ 위치에 패러티비트를 위치시킨다는 말이다.)
그러면, 송신단의 인코딩 값은 아래 표와 같이 제한된다.
| $p_1$ | $p_2$ | 데이타($d_1$) | 코드워드 |
| 0 | 0 | 0 | 000 |
| 1 | 1 | 1 | 111 |
표 7. 송신단에서의 유일한 인코딩 값
그리고 수신단을 조사해보면,
| 패러티($p_1$) | 패러티($p_2$) | 데이타($d_1$) | 코드워드 | 에러유무/에러위치/ MSB에서 위치 |
| 0 | 0 | 0 | 000 | 정상 |
| 0 | 0 | 1 | 001 | Error / 000 / 3번 |
| 0 | 1 | 0 | 010 | Error / 000 / 2번 |
| 0 | 1 | 1 | 011 | Error / 111 / 1번 |
| 1 | 0 | 0 | 100 | Error / 000 / 1번 |
| 1 | 0 | 1 | 101 | Error / 111 / 2번 |
| 1 | 1 | 0 | 110 | Error / 111 / 3번 |
| 1 | 1 | 1 | 111 | 정상 |
표 8. 수신단에서의 코드워드
신드롬을 체크한다.
$S_1=XOR(p_1, d_1)$
$S_2=XOR(p_2, d_1)$
아래의 표를 얻을 수 있는데,
| 패러티($p_1$) | 패러티($p_2$) | 데이타($d_1$) | 코드워드 | $S_1$ | $S_2$ | 비고 |
| 0 | 0 | 0 | 000 | 0 | 0 | 정상 |
| 0 | 0 | 1 | 001 | 1 | 1 | 3번 위치 에러 |
| 0 | 1 | 0 | 010 | 0 | 1 | 2번 위치 에러 |
| 0 | 1 | 1 | 011 | 1 | 0 | 1번 위치 에러 |
| 1 | 0 | 0 | 100 | 1 | 0 | 1번 위치 에러 |
| 1 | 0 | 1 | 101 | 0 | 1 | 2번 위치 에러 |
| 1 | 1 | 0 | 110 | 1 | 1 | 3번 위치 에러 |
| 1 | 1 | 1 | 111 | 0 | 0 | 정상 |
표 9. 수신단에서의 코드워드와 신드롬
신드롬에 대해서 정리하면,
| $S_1$ | $S_2$ | $S_1 S_2$ | 에러유무/에러위치 |
| 0 | 0 | 00 | 정상 |
| 0 | 1 | 01 | 에러/2번 |
| 1 | 0 | 10 | 에러/1번 |
| 1 | 1 | 11 | 에러/3번 |
표 10. 수신단에서의 신드롬
마지막으로 신드롬의 비트만 바꾸어 놓으면,
| $S_1$ | $S_2$ | $S_2 S_1$ | 에러유무/에러위치(MSB=1) |
| 0 | 0 | 00 | 정상 |
| 0 | 1 | 01 | 에러/1번 |
| 1 | 0 | 10 | 에러/2번 |
| 1 | 1 | 11 | 에러/3번 |
표 11. 수신단에서의 신드롬의 비트 역전
위 표처럼 에러유무, 정상판별 및 에러 발생 위치를 바로 알 수 있게된다.
(표 6과의 비교해서 그 차이점에 주목한다. 표 6의 신드롬 비트를 변경해도 신드롬 값이 나타내는 위치는 표. 11이 명확하다.)
그러면 데이타가 커지면 어떻케 해야 할까?
데이타의 갯수만큼 패러티를 하나씩 만들어서 송신해야 하나? 데이타가 4개면 4개의 패러티를 보내면 될 것 같기도 하다. 그런데… 이렇케 안하고 패러티 3개로 한다. 아래에 설명하겠다.
해밍코드
해밍코드는 프레임길이 7로 구성되는 데이타 4비트, 패러티 3bit로 구성되는 코드이다. 이 코드는 오류발생을 알수 있으며 또한 오류자동수정에 이용되는 코드이다. 줄여서 Hamming(7,4)로 표기한다.
해밍코드 기술에 수학적 기반에 대한 공부는 그냥 넘어가보자. 단, 패러티가 3개가 되는 이유는 패러티가 3개여야지 7개의 비트값 위치를 지정하는 코드, 그리고 정상이라는 코드까지 총 8개를 만들 수 있음은 이해를 해야 한다. (여기서 잠깐, 비정상이란 코드는 어떻케 만드나? 신드롬코드에 하나라도 1이 있으면 에러이다.)
그런데 패러티가 3개뿐이 없다. 4개면 될 것 같은데 3개라 어떡해야 할까?
4개의 모집단에서 3개씩 뽑아서 조합을 만들면 될 것 같다.
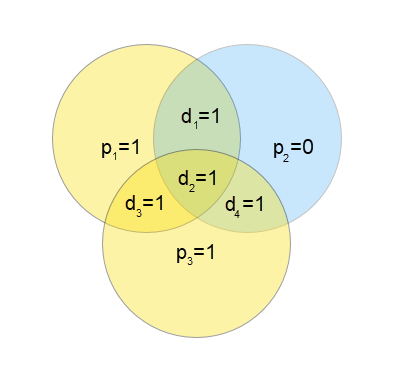
신드롬이 111이 되면, 3개의 교집합에 문제가 있음을 나타낸다. 신드롬이 101이 되면, 첫 번째와 세 번째에 문제가 있으나 이의 교집합인 $d_2$가 정상임을 나타낸다. 송신단에서의 유효코드는 아래와 같다.
| $d_1$ | $d_2$ | $d_3$ | $d_4$ | $p_1=XOR(1,2,3)$ | $p_2=XOR(1,2,4)$ | $p_3=XOR(2,3,4)$ | 코드워드 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0000 000 |
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0001 011 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0010 101 |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0011 110 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0100 111 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0101 100 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0110 010 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0111 001 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1000 110 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1001 101 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1010 011 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1011 000 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1100 001 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1101 010 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1110 100 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1111 111 |
표 12. 송신단에서의 유효코드(16개의 값 만을 가진다)
수신단에서의 신드롬은 아래와 같다.
$S_1=XOR(d_1,d_2,d_3,p_1)$
$S_2=XOR(d_1,d_2,d_4,p_2)$
$S_3=XOR(d_2,d_3,d_4,p_3)$
즉, 신드롬이란 정상 수신된 데이터로 만들어진 패러티와 전달받은 패러티의 XOR 연산이며 1이면 문제가 있음을 판별하는 방식이다.
이것을 해밍코드로 보낸다. 단, 패러티의 위치를 2의 배수의 위치로 변경하고 신드롬의 순서를 해밍 방법으로 바꾼다. 그러면 아래와 같은 코드표를 볼 수 있다.
| $p_1$ | $p_2$ | $d_1$ | $p_3$ | $d_2$ | $d_3$ | $d_4$ | 코드워드 | $S_1$ | $S_2$ | $S_3$ | 신드롬($S_3 S_2 S_1$) | 에러유무/에러위치 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0000 000 | xor(0,0) | xor(0,0) | xor(0,0) | 000 | 정상 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0000 001 | xor(0,0) | xor(1,0) | xor(0,1) | 011 | Err / 3 번째 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0000 010 | xor(1,0) | xor(1,0) | xor(0,1) | 111 | Err / MSB |
| … | … | … | … | … | … | … | … | … | … | … | … | |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1111 100 | xor(0,1) | xor(0,1) | xor(1,1) | 110 | Err / 6 번째 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1111 101 | xor(0, 1) | xor(1,1) | xor(0,1) | 101 | Err / 5 번째 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1111 110 | xor(1, 1) | xor(0,1) | xor(0,1) | 011 | Err / 3 번째 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1111 111 | xor(1, 1) | xor(1,1) | xor(1,1 ) | 000 | 정상 |
표 13. 해밍코드 및 신드롬
즉, 위와 같이 신드롬값을 보고, 에러유무 및 에러정정 기능을 수행할 수 있다.
마지막으로 아래의 문제를 풀어보자.
코드워드010 0111가 수신단에 들어왔다. 오류발생유무를 체크하고 오류비트의 위치를 찾아 원래의 코드로 변경하시오. 단, 해밍코드이다.
풀이 1)
패러티 비트는 1,2,4 번째 값. => $p_1=0, p_2=1, p_3=0$
데이타 비트는 3, 5, 6, 7 번째 값. => $d_1=0, d_2=1 , d_3=1 , d_4=1 $
$S_1 = XOR(d_1, d_2, d_3, p_1) = XOR(0, 0) =0$
$S_2 = XOR(d_1, d_2, d_4, p_2)=XOR(0, 1) =1$
$S_3 = XOR(d_2, d_3, d_4, p_3)=XOR(1, 0)=1$
신드롬비트는 110이 되며, MSB에서 6번째 비트를 반대로 하면 된다.
풀이 2)
윗 문제풀이는 지금은 기억할 수 있지만 나중에 이와 똑 같이 나오는 문제는 이런 방법을 기억 못할 수 있다. 그래서 문제가 나오면,
해밍코드 010 0111는 데이타(0111) +패러티(010)로 변경해서 쓴다.
| 코드워드 | $d_1$ | $d_2$ | $d_3$ | $d_4$ | $p_1$ | $p_2$ | $p_3$ |
| 해밍코드에서의 위치 | 3 | 4 | 5 | 6 | 1 | 2 | 4 |
| 값 | 0 | 1 | 1 | 1 | 0 | 1 | 0 |
표 14. 해밍코드의 간단 풀이 표
$XOR(d_1,d_2,d_3, p_1)=0$ > 1,2,3은 이상이 없다.
$XOR(d_1,d_2,d_4, p_2)=1$ > $d_4$가 에러거나 p_2에 이상이 있다.
$XOR(d_2,d_3,d_4,p_3)=1$ > $d_4$가 에러거나 p_3에 이상이 있다.
그러므로 1개의 에러가 발생하려면 $d_4$가 이상이 있어야 한다.
$d_4$는 6번째 위치하므로 6번 비트를 NOT 해주면 된다.
풀이 3)
또한 그림 3과 같이 그려서 밴다이어그램으로 풀어도 좋다.

그림 3에서 보듯이 $p_2$와 $p_3$가 불량하다. 그런데 $d_2$는 정상임을 좌상의 집합에서 이미 보이고 있다. 그러므로 $p_2$와 $p_3$의 공통 값 $d_4$가 문제임을 알 수 있다. 이걸 0으로 변경하면 모두 정상으로 바뀐다.
최종 정리하자면,
- 해밍코드는 코드워드 7비트, 데이타비트 4비트, 패러티비트 3비트를 사용한다.
- 해밍코드는 에러의 발생 및 에러의 수정이 가능한 코드이다.
- 2개의 비트오류를 감지할 수 있다. (본 포스팅에서는 설명하지 못하였다)
- Hamming(7,4)로 간략히 표시 가능하다.
- 패러티는 자리수를 정하는 수로 생각하고 1과 2의 배수에 꼭 위치시킨다.
- 나머지 자릿수는 데이타비트로 채운다.
- 신드롬은 역순으로 써준다.
- 그리고 해밍코드 문제는 밴다이어그램을 그리면 쉽게 그 답을 찾을 수 있다.