부제: 물리와 공학의 언어: 벡터, 그리고 복소평면의 비밀
물리학이나 공학을 공부하다 보면 필연적으로 마주치는 개념이 바로 ‘벡터(Vector)’다. 네이버 지식백과에서는 벡터를 “위치, 속도, 힘 등과 같이 크기와 방향성을 갖는 물리량을 나타내는 기하학적 대상”이라고 정의한다.
단순히 크기만 있는 ‘스칼라(예: 온도, 질량)’와 달리, 벡터는 어느 방향으로 작용하는지가 매우 중요하다. 이 벡터를 우리가 익숙한 xy 평면에서 시작해, 더 강력한 도구인 ‘복소평면’으로 확장해보고 그 안에 숨겨진 놀라운 비밀까지 파헤쳐 본다.
1. 익숙한 시작: xy 평면에서의 벡터
먼저 가장 기본적인 2차원 xy 평면에서 힘(Force)을 예로 들어 벡터를 표현해 보자. 단위는 뉴턴[N]을 사용한다.

- 상황 1: 정방향으로 밀기
- 어떤 물체를 오른쪽(x축 방향)으로만 5[N]의 힘으로 민다고 가정해 보자. 이는 원점에서 시작해 x축으로 5만큼 뻗어 나가는 화살표로 아주 간단하게 나타낼 수 있다. 좌표로는 (5, 0)이 될 것이다.
- 상황 2: 비스듬히 밀기
- 이번에는 5[N]의 힘으로 비스듬히 밀어본다. 만약 우리가 잘 아는 3:4:5 비율의 직각삼각형을 염두에 두었다면, 이 힘은 x축 방향으로 3만큼, y축 방향으로 4만큼의 힘이 합쳐진 결과다. 좌표평면에서는 원점과 점 (3, 4)를 잇는 화살표로 표현된다.
이처럼 화살표를 이용해 크기와 방향을 나타낸 것을 우리는 ‘벡터’라고 부른다. 여기까지는 우리가 익히 아는 $y=f(x)$ 관계를 다루는 2차원 실수 공간에서의 이야기다.
2. 차원을 넘어: 복소평면(Complex Plane, 가우스 평면)으로의 확장
이제 시야를 조금 넓혀보자. 기존 xy 평면에서 x축은 그대로 실수축(Real axis)으로 두고, y축을 허수축(Imaginary axis, $i$ 또는 $j$축)으로 변경하면 ‘복소평면’이 된다.
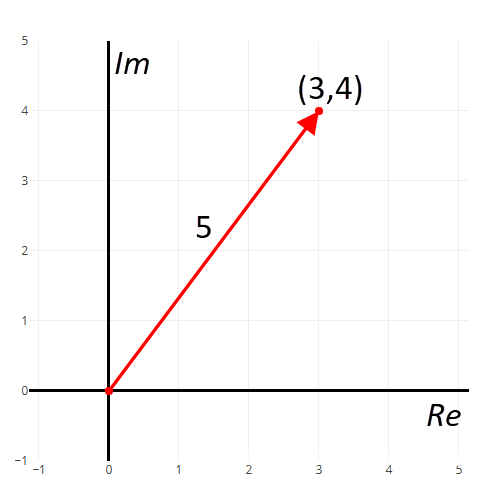
앞서 본 (3, 4) 벡터는 복소평면에서 $3 + 4i$ (또는 $3 + 4j$)라는 복소수로 표현된다.
“굳이 왜 복잡해 보이는 복소평면으로 옮기는 걸까?”
가장 큰 이유는 연산의 편리함 때문이다. 벡터를 복소수로 표현하면 벡터 간의 덧셈이나 뺄셈을 할 때, 실수부는 실수부끼리, 허수부는 허수부끼리 묶어서 계산하기가 매우 수월해진다. 공학, 특히 전기전자 공학에서는 허수 단위를 전류 $i$와 구분하기 위해 $j$를 주로 사용하며, 복소평면은 벡터를 다루는 표준적인 도구가 되었다.
3. 복소평면의 첫 번째 비밀: 오일러와 회전(Rotation)
그런데 단순히 계산이 편하다는 이유만으로 복소평면을 쓰는 것은 아니다. 복소평면은 벡터를 동적으로 다룰 수 있는 강력한 무기를 숨기고 있다.
그 비밀의 열쇠는 바로 ‘오일러의 공식(Euler’s formula)’이다.
$$e^{ix} = \cos x + i \sin x$$
(단, $x$는 실수)
이 식에서 $x$에 $\pi$(파이)를 대입하면 그 유명한 $e^{i\pi} = -1$이라는 아름다운 항등식이 나온다.
하지만 더 중요한 것은 이 공식이 의미하는 ‘기하학적 행동’이다. 복소평면에서 어떤 복소수에 $e^{ix}$를 곱한다는 것은, 그 벡터를 원점을 중심으로 반시계 방향으로 $x$라디안만큼 더 회전시킨다는 뜻이다. 이건 $1+0j$ 벡터에 $e^{ix}$를 곱하면 $x$라디안 만큼 회전함을 생각하면 이해가 쉬울 것이다.
또는 $x$값에 $0, \frac{\pi}{4}, \frac{\pi}{2}, \dots, 2\pi$를 순서대로 넣어보면, 그 벡터가 놓이는 점이 복소평면 위에서 원을 그리며 뱅글뱅글 도는 모습을 볼 수 있다. 즉, 복소평면은 ‘회전’을 표현하는 데 최적화된 공간이다.
4. 복소평면의 두 번째 비밀: 회전의 속도, 주파수(Frequency)
회전이 가능하다면, 자연스럽게 ‘얼마나 빨리 도는가?’에 대한 질문이 생긴다.
앞선 오일러 공식의 실수 $x$를 연속적으로 흐르는 시간 $t$로 바꿔보자. 그리고 회전하는 속도(각속도)를 나타내는 각주파수 $\omega_0$ (오메가 제로)를 도입하면 다음과 같은 식이 탄생한다. ($\omega_0 = 2\pi f_0$)
$$v(t) = e^{ j \omega_{0} t} = e^{j 2 \pi f_{0} t}$$
- $i$ 대신 공학에서 주로 쓰는 $j$를 사용했다.
이 식은 무엇을 의미할까? 바로 시간 $t$가 증가함에 따라, 각주파수 $\omega_0$의 일정한 속도로 복소평면 위를 회전하는 벡터 함수를 나타낸다. (여기서 진폭은 1로 가정)
이것이 바로 우리가 일상에서 접하는 교류 전압, 전파 신호 등의 파동을 수학적으로 표현하는 가장 핵심적인 방법이다. 정지해 있던 화살표(벡터)가 복소평면과 오일러 공식을 만나 시간의 흐름에 따라 역동적으로 회전하는 신호가 된 것이다.
마무리하며
xy 평면에 멈춰있던 정적인 힘의 화살표가 복소평면으로 넘어오면서 계산의 편리함을 얻었고, 오일러의 공식을 만나 회전하는 역동성을 얻었다.
이처럼 복소평면은 단순한 좌표계를 넘어, 회전과 주기적인 현상(주파수)을 다루는 물리학과 공학의 필수 불가결한 언어다. 즉, 벡터 평면에서 실수축과 서로소인 관계로써 벡터의 연산을 쉽게 하는 도구로 생각했던 복소 평면이 실제로는 세상을 설명하는 수식을 담아내는 칠판이라는 점이 매우 놀랍게 다가온다.
2026. 1.13 표준문서화 됨