허수는 2차 방정식의 근의 공식에 넣어서 풀다보면 나타났으나 이는 기하학에 위배되므로 철저히 무시되었다. 근의 공식이란 “정사각형 면적(근)을 만들기 위한 한 변의 길이가 얼마?“라는 문제인데, 면적이 ‘음수’가 될 수 없으므로 해가 절대로 존재할 수 없다는데 모두 동의하였기 때문이다.
그러다 허수는 3차 방정식의 해법의 역사를 통해서 드러나게 된다. 이 역사는 16세기 이탈리아 르네상스 시기에 벌어진 지적 소유권 분쟁, 공개 수학 대결, 그리고 배신으로 점철된 드라마다. (유투브의 EBS 채널에 이러한 내용이 올라와 있다.) 그리고 이 과정에서 대수학(Algebra)이 기하학에서 독립, 또한 인류가 허수(Imaginary Number)의 존재를 처음으로 인식하게 된 계기가 되었다.
1. 시대적 배경: 수학은 ‘밥그릇’이었다
당시 수학자들은 자신의 발견을 논문으로 공개하는 현대와 달리, 비법을 철저히 숨겼다. 특정 유형의 방정식을 풀 수 있다는 것은 후원자를 얻거나 대학 교수직을 유지하는 강력한 무기였기 때문이다. 이들은 광장에서 돈을 걸고 서로 문제를 내며 승부를 가리는 ‘수학 결투’를 벌이곤 했다.
2. 주요 등장인물과 사건의 전개
1막: 최초의 발견자, 델 페로 (Scipione del Ferro)
볼로냐 대학의 교수였던 델 페로는 $x^3 + px = q$ 형태(이차항이 없는 특수한 형태)의 해법을 최초로 발견했다. 하지만 그는 이 비법을 뺏길까 두려워 죽기 직전 제자 안토니오 피오르(Antonio Fior)에게만 몰래 전수하고 사망했다.
2막: 말더듬이 천재, 타르탈리아 (Niccolò Tartaglia)
피오르는 스승의 비법만 믿고 당대 최고의 실력자였던 타르탈리아에게 도전장을 던졌다. 타르탈리아는 스스로의 힘으로 $x^3 + px^2 = q$ 형태를 풀 줄 알았는데, 결투 직전 델 페로의 형태($x^3 + px = q$)까지 일반화하는 데 성공했다.
결과적으로 타르탈리아는 피오르가 낸 모든 문제를 풀었지만, 피오르는 타르탈리아의 문제를 하나도 풀지 못해 타르탈리아가 완승을 거뒀다.
3막: 카르다노의 등장과 배신 (Gerolamo Cardano)
이 소식을 들은 밀라노의 의사이자 수학자 카르다노는 타르탈리아에게 접근했다. 온갖 감언이설과 “절대 비밀로 하겠다”는 기독교적 맹세를 한 끝에 해법을 전해 들었다.
그러나 카르다노는 델 페로가 타르탈리아보다 먼저 해법을 발견했다는 기록을 찾아냈다. 그는 “타르탈리아와의 맹세는 유효하지만, 델 페로의 업적을 공개하는 것은 맹세 위반이 아니다”라는 논리로 1545년, 그 유명한 저서 “아르스 마그나(Ars Magna)”에 그 해법을 적어 세상에 공개해 버렸다.
3. 카르다노의 공식 (Cardano’s Formula)
카르다노가 정리한 3차 방정식의 근의 공식은 다음과 같다. $x^3 + px + q = 0$ 꼴로 변형된 방정식의 해는 아래와 같이 표현된다.
$$x = \sqrt[3]{-\frac{q}{2} + \sqrt{\frac{q^2}{4} + \frac{p^3}{27}}} + \sqrt[3]{-\frac{q}{2} – \sqrt{\frac{q^2}{4} + \frac{p^3}{27}}}$$
4. 실근이지만 허수 형태를 가짐: 멘탈의 붕괴
3차 방정식의 근의 공식(카르디노)을 적용하다 보면, 명백히 실근이 3개 존재하는 경우임에도 불구하고 계산 과정 중간에 $\sqrt{-1}$과 같은 음수의 제곱근이 튀어나오는 현상이 발생했다.
즉, $x^3 – 15x – 4 = 0$ 의 사례를 를 보면, 직관적으로 $x=4$를 대입하면 식이 성립한다.
$$4^3 – 15(4) – 4 = 64 – 60 – 4 = 0$$
즉, 이 방정식은 명백한 실근 4를 가지고 있다. 나머지 두 근도 모두 실수다. ($x = -2 \pm \sqrt{3}$)
그런데 이 식을 카르다노의 공식에 집어넣으면 아주 기괴한 일이 벌어진다. 카르다노의 공식에 $p=-15, q=-4$를 넣고 계산하면 다음과 같은 식이 나온다.
$$x = \sqrt[3]{2 + \sqrt{-121}} + \sqrt[3]{2 – \sqrt{-121}}$$
루트 안에 음수($-121$)가 있다. 즉, $11i$가 튀어나온다.
$$x = \sqrt[3]{2 + 11i} + \sqrt[3]{2 – 11i}$$
답은 분명히 4인데, 공식은 “허수 덩어리를 내놓는 상황”이 된 것이다. 당시 수학자들은 이 지점에서 멘탈이 붕괴되었다. 실수를 구하는데 허수가 필요하다니?
5. 허수의 탄생(인정): 터널로 봄
그 때 이것을 해결한 사람이 바로 라파엘 봄벨리(Rafae Bombelli)다. “혹시 저 세제곱근 덩어리 자체가 어떤 복소수이지 않을까?”
그는 셜록 홈즈식으로 “결과가 있으면 원인은 분명히 있다”라는 방식으로 문제를 접근해서 아래와 같이 풀이를 남겼다. 먼저 $(2+i)^3$을 전개해 보자.
$$(2+i)^3 = 2^3 + 3(2^2)(i) + 3(2)(i^2) + i^3$$
$$= 8 + 12i – 6 – i = 2 + 11i$$
놀랍게도 $\sqrt[3]{2+11i}$는 $2+i$였고, 반대쪽 $\sqrt[3]{2-11i}$는 $2-i$였다. 이를 원래 식에 대입하면 허수 부분이 마법처럼 사라진다. 그는 이를 위해 허수를 포함한 수라는 의미로 복소수(Complex Number: $a+bi$)를 제안했다.
$$x = (2+i) + (2-i) = 4$$
결국 수학자들은 “실수 해(목적지)에 도달하기 위해 잠시 허수(터널)를 통과해야 한다”고 이해했고 ‘허수’를 받아들이게 되었다.
즉, 이 때문에 허수는 3차 방정식의 연구 드라마를 통해, 비로소 “수의 지위”를 얻게 되었다.
6. 오일러: 테일러 급수로 오일러 정리를 발표
오일러는 초월함수의 테일러급수 표현에 대해서 많은 연구를 하였다. 초월함수라는 것은 대수적으로 그 값을 구할 수 없는 함수이다. 대수적이라는 말은 사칙연산과 거듭제곱의 형태로 표현할 수 없는 함수를 말한다. 대표적으로 로그함수, 삼각함수 및 지수함수 등이 있다.
[1] 지수함수
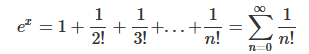
[2] 코사인 함수
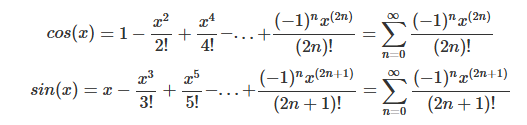
$cos(x)$는 우(偶)함수(짝수항만 있다.)이고 번호가 교차한다. $sin(x)$는 기(奇)함수(홀수 항만 있다)이고 부호가 교차한다.
즉, $cos(x)$는 다항식의 짝수항 만, $sin(x)$는 홀수항 만 써 놓은 후 삼각함수가 +와 -로 순환하는 것을 그대로 써 놓으면 된다. 물론 차수의 팩토리얼로 나누어주는 것은 기억해야 된다.
벌써 냄새가 난다. 부호가 교차하는 이유는 허수를 2 번 곱해서가 아닐까? 오일러는 이런 생각이 들었는지 아니면 그냥 했는지는 몰라도, $x$대신에 $ix$를 대입해서 테일러 전개를 구했다.
[3] $x$ 대신 $ix$를 대입
이제 지수함수 $e^x$의 $x$ 자리에 과감하게 허수 $ix$를 대입해 보자. 여기서 허수 단위 $i$의 거듭제곱 성질($i, -1, -i, 1$의 순환)이 핵심 역할을 한다.
$$e^{ix} = 1 + \frac{(ix)}{1!} + \frac{(ix)^2}{2!} + \frac{(ix)^3}{3!} + \frac{(ix)^4}{4!} + \frac{(ix)^5}{5!} + \cdots$$
$$e^{ix} = 1 + ix – \frac{x^2}{2!} – i\frac{x^3}{3!} + \frac{x^4}{4!} + i\frac{x^5}{5!} – \cdots$$
[4] ‘실수부’와 ‘허수부’로 헤쳐 모여!
이제 위 식에서 $i$가 없는 항(실수부)과 $i$가 있는 항(허수부)을 따로 묶어보자.
$$e^{ix} = \left( 1 – \frac{x^2}{2!} + \frac{x^4}{4!} – \cdots \right) + i \left( x – \frac{x^3}{3!} + \frac{x^5}{5!} – \cdots \right)$$
로 전개된다.
[5] 결론: 잃어버린 조각을 찾았다
윗 식을 자세히 보면,
- 첫 번째 괄호는 정확히 $\cos x$의 테일러 급수와 같다.
- 두 번째 괄호는 정확히 $\sin x$의 테일러 급수와 같다.
그러므로 우리는 다음과 같은 결론에 도달한다.
$$e^{ix} = \cos x + i \sin x$$
[6] 오일러의 항등원
윗 오일러 정리의 x에 $\pi$를 넣으면 된다.
$$e^{i \pi} =cos(\pi) + i sin(\pi)$$
$$e^{i \pi}=-1$$
[7] 항등원이 말하는 것
오일러는 오일러의 항등원을 가지고, 대수적으로는 성립함을 보였으나, 이것이 회전이라는 의미를 가진다는 것은 설명하지 못한것으로 보인다. 이 회전의 의미와 기하학적의미는 가우스에게 공이 넘어가게 되었다.
7. 가우스: 가우스 평면(기하에서의 표현)
가우스는 정17각형은 자와 컴퍼스만으로 작도가 불가능함을 인지했는지는 몰라도(자는 1차원, 컴퍼스는 2차원 도구이기 떄문이라 설명), 이 문제를 기하학에서 대수학으로 이동시켜서 해결할 수 있게 되었다.
그 방법을 설명하기 전에 아래 이야기를 먼저 해 보자. 아래는 2차 방정식의 해를 나타낸 그래프이다.

그림 1의 2차 방정식의 해는 실수 평면에서는 무의미하다. 그런데 이걸 허수 평면(복소수 평면, 가우스 평면)으로 옮긴 후 나타내면 (1,0)을 꼭지점으로 하는 정삼각형이 나타난다. 또한, 반지름 1인 원을 정확히 3등분하는 것을 알 수 있다. 왜 (1,0)을 포함해서 이야기 했을까?
원래 $x^2 + x +1$ 함수는 $x^3=1$을 인수분해 하면 만들어지는 2차 다항식이기 때문이며 여기서 그 3차 방정식의 해는, $1, -\frac{1}{2} + \frac{\sqrt{3}}{2}, -\frac{1}{2} -\frac{\sqrt{3}}{2}$ 3개이며 이건 삼각형의 3 꼭지점 좌표를 나타내고 있다.

4차도 알아보자. $x^4=1$의 해를 구하면,

단위원에서 4개의 꼭지점을 연결하는 정사각형이 나타난다.
음… 이제 17각형도 이렇케 풀면 되는게 아닌가? 이것이 바로 가우스의 업적이다.
즉, 가우스는 정17각형은 “작도가 불가능하다고 여겨졌던 정17각형이 작도 가능함을 대수적으로 증명했다”
그래서 그는 $x^{17}=1$의 해를 풀고, 그 해를 연결한 선이 정17각형이라는 것을 보여주었으며, 이것이 바로 허수(복소수)가 자연과 밀접한 관련이 있는 유의미한 숫자로 다가오게 하는 계기가 되었다.
또한 가우스는 오일러의 항등원이 기하에서는 회전을 의미함을 명확하게 보여주어서 대수학과 기하학을 연결해주는 쾌거를 달성했다.
끝으로 정다각형은 어떻게 만드냐면, (1,0)에서 시작해 단위원을 같은 크기만큼 이동하면서 만들면 된다. 만일 호도법이 없었다면, 이러한 호의 이동거리를 균일하게 만들면서 이동하기가 매우 어려웠을 것이다. 호도법은 오일러도 오일러 정리를 발표할 때 유용하게 사용하던 좋은 도구였다.
8. 추가 내용(반은 헛소리…)
실수에서의 곱은 면적이 되지만 복소평면에서는 회전량이 된다. 그런데, 왜 회전량을 우리의 수 체계에서 갑자기 보여주는지 그 이유는 모르겠다.
본인은 아래처럼 생각해 보았다.
- 마치 2차 이상의 방정식이 원래부터 복소수의 형태를 가진 방정식였으며,
- 실수 해만 가진다는 것은 “단위 원”과 “회전”과 관련이 없는 원주 운동하지 않는 특별한 시스템이다.
- 그러므로 <1번>과 <2번>의 단언에 따르면, 포물선 및 다차원 함수 중 복소수를 가지는 방정식은,
- 모두 원에서 출발한 함수이고, 이는 이 원의 원주에 꼭지점을 가지는 해를 가진다고 볼 수 있다.
- 그러므로 $x^2$ 차원 및 그 이상 차원의 형태는 원래 원에 회전을 추가해주는 도구였는데,
- 차원이 커가도 (x를 더 곱해도) 기존의 원은 사라지지 않고 원의 크기?와 회전만 추가된다.
- 그래서 회전하다가 보니 처음 시작한 자리$(1, 0j)$로 돌아오려면? (우리가 실수값 $y=0$을 만족하는 $x$를 구하라고 했기 때문이다)
- 바로 그 회전량을 만족시키기 위해서 거쳐야 되는 점들을 찾은것이 아닐까?
- 만일 그렇다면, 2차 방정식에서 $(0, j)를 만족하는 회전량을 찾는 해를 구하라고 하면 찾을 수 있을까?
- 또한 그 해가 실수로만 이루어지면 이를 xy 평면상에서도 그릴 수 있을까?